Intersection of a line and a sphere Intersection of a Line and a sphere calculator ▲
Parametric line equation L1: x = + t
y = + t
z = + t
Line equation L1: x +
= y +
= z +
Lines defined
by 2 points		 L1: x1 y1 z1
x2 y2 z2
Line defined
by vector		 L1:
Vector: i + j + k
Point: x: y: z:
Sphere of the form:     (x − a)2 + (y − b)2 + (z − c)2 = r2
( x - )2 + ( y - )2 + ( z - )2 = 2
Sphere of the form:     x2 + y2 + z2 + Ax + By + Cz + D = 0
x2 + y2 + z2 + x + y + z + = 0
First intersection point:
 
Second intersection point:
 
Distance between intersections:
 
              
Sphere and line intersection Print sphere line intersection summary ▲
Line given by parametric form is:
x = x1 + (x2 − x1)t
y = y1 + (y2 − y1)t
z = z1 + (z2 − z1)t
(x − xc)2 +(y − yc)2 + (z − zc)2 = r2
Substituting line values x, y and z into the equation of the sphere gives a quadratic equation of the form:         at2 + bt + c = 0
a = (x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2
b = − 2[(x2 − x1)(xc − x1) + (y2 − y1)(yc − y1) + (zc − z1)(z2 − z1)]
c = (xc − x1)2 + (yc − y1)2 + (zc − z1)2 − r2
The solution for  t  is: t=(-b±√(b^2-4ac))/2a
Condition for intersection: b2 − 4ac > 0
Condition for tangency: b2 − 4ac = 0
No intersection when: b2 − 4ac < 0
The intersection points can be calculated by substituting  t  in the parametric line equations.
Example: find the intersection points of the sphere
(x − 1)2 ⧾ (y − 4)2 ⧾ z2 = 16
with the line given by
x = 1 ⧾ t,       y = 2,       z = 3 − 2t
First find the values of the coefficients  a, b  and  c:
a = (1)2 ⧾ (0)2 ⧾ (− 2)2 = 5
b = − 2[(1)(1 − 1) ⧾ (0)(4 − 2) ⧾ (− 2)(0 − 3)] = − 12
c = (1 − 1)2 ⧾ (4 − 2)2 ⧾ (0 − 3)2 − 16 = − 3
The quadratic equation is: 5t2 − 12t − 3 = 0
x1 = 1 ⧾ 2.63 = 3.63 y1 = 2 z1 = 3 − 2 • 2.63 = − 2.26
x2 = 1 − 0.23 = 0.77 y2 = 2 z2 = 3 ⧾ 2 • 0.23 = 3.46
And the intersection points are:
(3.63, 2, − 2.26) and (0.77, 2, 3.46)
Sphere and line detail equations solution Print sphere line intersection summary ▲
Find the intersection points of the parametric line given by the equations:
x = x1 + (x2 − x1)t y = y1 + (y2 − y1)t z = z1 + (z2 − z1)t
and the sphere given by the equation: (x − xc)2 +(y − yc)2 + (z − zc)2 = r2
Because the intersection points of the parametric equations should satisfy the sphere equation we will substitute the values of  x y  and  z  of the parametric equations into the sphere equation:
[(x2 − x1)t − (xc − x1)]2 ⧾ [(y2 − y1)t − (yc − y1)]2 ⧾ [(z2 − z1)t − (zc − z1)]2 = r2
Now we will find the square values of the parenthesis.
(x2 − x1)2t2 − 2t(x2 − x1)(xc − x1) + (xc − x1)2 + (y2 − y1)2t2 − 2t(y2 − y1)(yc − y1) +
(yc − y1)2 + (z2 − z1)2t2 − 2t(z2 − z1)(zc − z1) + (zc − z1)2 − r2 = 0
Arranging the expression received as a powers of  t  we get:
t2[(x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2] −
2t[(x2 − x1)(xc − x1) + (y2 − y1)(yc − y1) + (z2 − z1)(zc − z1)] +
(xc − x1)2 + (yc − y1)2 + (zc − z1)2 − r2 = 0
And we got a quadratic equation of the form:       at2 + bt + c = 0
Where: a = (x2 − x1)2 + (y2 − y1)2 + (z2 − z1)2
b = − 2[(x2 − x1)(xc − x1) + (y2 − y1)(yc − y1) + (z2 − z1)(zc − z1)]
c = (xc − x1)2 + (yc − y1)2 + (zc − z1)2 − r2
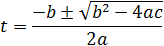The solution for  t  is: t=(-b±√(b^2-4ac))/2a
Substitute this values of  t  into the parametric line equations to get the intersection points.